1. 　総人口に対する都市人口の割合の一定性と順位による都市人口の規則性
　都市人口を十大都市人口と定義した場合、総人口と一定の関係を持つことが見いだされた。この規則性を生み出すと思われる、都市人口の順位規模分布の法則性は既に他の研究者が報告しているが、ここではまず、その順位規模分布の法則をより多くの時代や地域で用い得るよう一般化した。さらにその法則が都市のみならず、集落一般に適用可能なことを示し、そのことから十大都市人口と総人口の間に一定の比例定数があるという関係を導き出した。

1.1 　総人口に対する都市人口の割合の一定性
　一般に、20世紀は世界で都市化が大きく進行した、とされている。国連による1950年から2005年までの農村・都市人口データ(United Nations 2004a)によれば、世界の総人口に対する都市人口割合は1950年の29.1%から2005年の49.2%まで増加したことを示している (表 ‎III 1)。

表‎III-1　世界農村・都市人口及び割合

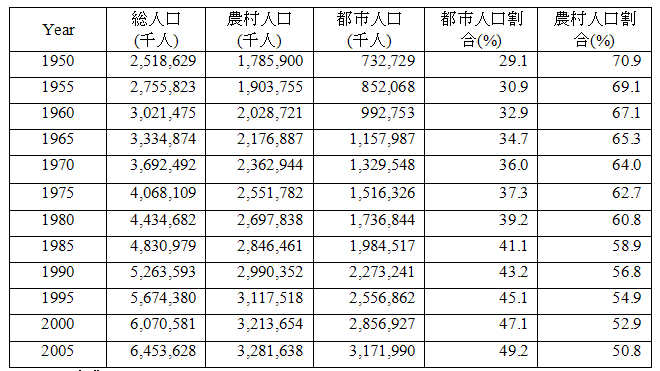出典 : World Urbanization Prospects : The 2003 revision, UN, Department of Economic and Social Affairs, Population Division

　しかしこの国連データの「都市」の定義は、各国独自の都市の定義に従っていて、ある共通の都市の定義が使用されたわけではない⁷ 。そのため世界全体の都市人口とは、200人でも「都市」となる北欧の国々の都市人口と、50,000人以上の町でないと「都市」にならない韓国の都市人口を集計して計算されたというものである。したがって、確かに時系列的に各国の定義が変わっていないとすれば、「都市化」が進んでいると考えられるが、各国でここまで異なって定義されている「都市」は、「農村」と比べ歴然とした違いがあるわけではなく、その定義は極めて曖昧なものであるといわざるを得ない。
　そこで本論文では、「都市人口」を「上位x位の都市人口の合計」と定義した。x=10の場合、つまり上位十位の都市人口の合計（以下「十大都市人口」とする）を世界全域について計算すると、表 ‎III -2に示されるようにその総人口に対する割合（以下「十大都市人口割合」とする）は、1950年から2000年の間に2.69%から2.74%と、ほぼ一定であった。これは、前述した国連定義の「都市人口」がこの期間に29.1%から47.1%と大幅に上昇したのと対照的である。

表‎III-2　世界の十大都市人口とその割合(1950～2000年)

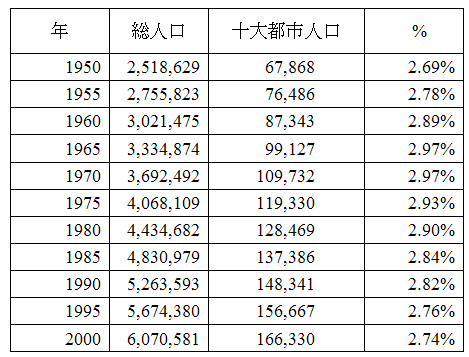注: 総人口(千人)、十大都市人口(千人)、% : 十大都市人口の総人口に対する割合(%)
出典 :総人口はWorld Population Prospects: The 2002 Revision、都市人口はWorld Urbanization Prospects : The 2003 revision

　これは、都市の形成には一定の秩序があり、総人口に対応して大都市の規模がその秩序に従って決定されているとみなせる。都市化が進んだとされる20世紀後半においても、このように定義された都市人口、つまり上位x位の都市人口合計の割合が一定であることについては、これまで論じられてこなかった。

1.2 　順位別にみた都市人口の法則性
　ある地域や国における都市人口の分布の規則性に関しては、順位規模法則（Rank Size Rule）として早くはAuerbach(1913)やZipf(1949)により提唱されてきた。この順位規模法則とは、調和分布(Harmonic Distribution)とも呼ばれ、

・・・式(1)

と示される。
　例えば、日本の2000年の人口集中地区(DID)人口について順位規模分布をみると、その分布は高い直線性を持ち（R2=0.9703）、その傾きは0.9466ときわめて1に近く、順位規模の法則が現在の日本都市人口で成り立っているといえる(図 ‎III-1)。

図 ‎III-1　日本都市(DID)人口の順位規模分布（2000年）

　これまでの一連の順位規模分布の研究では、この順位規模の傾きが1に近づくのは、自由主義体制下の成熟した社会である場合だとされ、それとの逸脱から社会の動向を解釈することが多く行われてきた。例えばBerry(1961)は、ラテンアメリカの植民地化の段階で、当初農村だけのところに植民地政府が作られたときは、その所在地が最大都市で、その人口は飛びぬけて大きくなり、順位規模の傾きは大きい。しかし次第に農村が階層化され人口が増える集落が出現し、それらが中型都市となると、順位規模の傾きが小さくなり、傾きが1に近づくという。またSkinner(1977)によれば、18世紀の中国は、首都である北京が飛びぬけて大きく、そのために順位規模の傾きが大きくなっていることを示した。逆に、近代以前のヨーロッパの都市人口(de Vries1995)や多くの地域人口 (Russell1958など)につい2て、都市、もしくは集落の人口規模の大小の差が少なく、順位規模の傾きが小さいことが指摘されている。
　本研究で収集した歴史上の都市人口データにおいても、その順位規模の傾きは、常に1であるわけではなく時代によって変化している。この順位規模の傾きは、ある時代、地域の都市人口構造を現す変数であると考え、順位規模分布を表す式(1)を次式のように一般化した。

・・・式(2)

　この式によれば、第n位の都市人口は、第1位の都市人口と順位規模分布の傾きaにより求めることができる。例えば最大都市100万人の場合の傾きaを変化させた場合の2位以下都市人口は図 ‎III-2のようになる。

図 ‎III-2　傾きaを変化させた順位規模分布 (モデル図)

　2000年の世界上位100位までの都市人口順位規模分布は、傾きaが0.5791で、R2=0.9608の高い直線性を持ち、一般的な順位規模分布の法則が成り立っていると判断できた(図 ‎III-3)。

図 ‎III-3　世界都市人口順位規模分布 (2000年世界)　

1.3 　集落全体への拡張
　これまでの都市人口の分析においては、都市と農村は異なったものであると区別されてきた。しかし都市も農村も複数の世帯で構成された「集落」であることには変わりなく、また都市と農村をどこで区別するかは明瞭ではない。そこで「集落」として、巨大都市から小さな村に至る、人間が生活する集団の全てを含むものであると定義する。
　順位規模分布の法則は、これまで都市、つまり大型の集落についてのみ論じられてきたが、集落全体についても同様に成り立つだろうか。
　日本の市町村という区分は、本来「市及び区はまとめて市部として、町及び村は郡部として、それぞれ都市的地域又は農漁村的地域を表すもの」(統計局2006) とされており、市、町、村、それぞれの人口は、近似的に集落の人口を表し、市町村人口分布は集落人口分布に近似すると考えることができよう。市町村人口の順位規模分布を観察すると（図 ‎III-4）、全部で3223ある市町村のうち、2500位程度までは、連続的な直線に近い分布を示している。つまり、上位都市人口で観察された順位規模分布の法則は、大都市から人口5,000人程度の村まで、ほぼ集落全体について同じように成り立っていることがわかった。

図 ‎III-4　日本の市町村別人口分布 (2000年)

　同様に、フランスでも日本の市町村に似た行政区分としてコミューン(commune)があり、このコミューン別に順位規模分布を見ると(図 ‎III-5)、日本の市町村人口分布で観察されたのと同様に、合計36,570個あるコミューンの上位30,000位までのコミューンについては、連続的な直線分布となり、一般的な順位規模の法則が成り立っている。

図 ‎III-5 フランスコミューンの順位規模分布（1999年）

　日本の市町村では、約2,500位以下、フランスコミューンであれば30,000位以下の小さな集落は、連続した傾向を持っていない例外であるが、この部分の総人口に対する割合は、日本では1.8%、フランスでは1.0%に過ぎない。したがって、この部分は全体人口の割合からみれば無視できるほどの規模であるとみなした。
　以上の日本、フランスの事例が一般的に当てはまると仮定すると、一般的な順位規模分布の法則は都市だけではなく集落全体について成り立っているといえる。集落人口の総和はその地域の総人口であるので、総人口と順位別の集落人口には一定の秩序が存在するということになる。

1.4 　一般的順位規模分布の法則により定義される都市構造
　式(2)で表した一般的な順位規模分布の法則が集落全体について当てはまるとすると、順位規模分布の傾きaと総集落数Nを与えれば、最大集落（最大都市）から最小集落までの相対的な人口規模を求めることができる。総人口は集落人口の総和として求められるので、総人口に対する上位集落人口、つまり上位都市人口の割合も、式（2）により計算することができる。順位規模分布の傾きaと集落数Nを変数として、上位x位の都市人口割合を計算すると、表 ‎III-3のようになった。

表‎III-3　一般的な順位規模分布の法則による上位都市人口割合

　つまり、集落数Nと順位規模分布の傾きaが一定のときは、上位x位の都市人口割合は一定となるが、集落数Nと傾きaが変化すると都市人口割合も変化する⁸ 。集落数Nが増える時、また傾きaが小さくなる時に上位x位都市人口割合が小さくなるという関係がある。この集落数Nと順位規模分布の傾きaを「都市人口構造」と定義すると、都市構造が一定であるときには、上位x位都市人口割合は一定であるといえ、また1950年から2000年の世界人口では十大都市人口割合がほぼ一定であったので、この期間の世界全体で見た場合の都市人口構造は不変であったということができる。

7. 「都市」となる基準人口は、最低200人から最高5万人までと幅広く、82ヶ国・地域の都市基準人口の平均は4420人であるが、最も多くの国に採用されている都市人口基準値は2000人である。都市の条件として、非農業従事者の割合の最低値を設けている国もあり、舗装道路、上下水道、医療・教育施設といった都市施設を備えていること、家と家の間隔が200m以下であること、といった要件を挙げているところもある。また、人口数ではなく、世帯数が100以上、といった条件を設定している国もある。

8. 集落人口を式（2）で定義した時の総人口はゼータ関数であり、傾きaが1より大きい時は収束値を持つ。そのため、表 ‎III 3において傾きaが1.5や2.0の場合は、Nが変化しても上位x位都市人口割合はほぼ不変である。